Full Simulation could be found HERE.

In this study, we were tasked with exploring the modeling of a dynamic system, specifically examining the differences between a Gillespie simulation and a mean field approximation of the same system.

Given that the Gillespie method involves stochastic simulations, I replicated each scenario 100 times to determine the system’s average trajectory. This average trajectory is depicted in the subsequent figure as faint solid lines accompanied by a shaded area. The faint lines illustrate the average path for certain initial conditions, while the shaded area indicates two standard deviations from the mean.

On the other hand, the dashed lines in the figure represent mean field simulations, which were performed using Euler integration. Both representations are superimposed for the purpose of comparison. Ideally, if both methods were in agreement, we would observe the dashed and solid lines of the same color aligning perfectly. Nevertheless, the results demonstrate a clear divergence between the two approaches.

Part Analytical Work:

1.1 Mean-field Equation

1.2 System Equilibria and stability

Setting \(\dot{B}\) to 0, so we get \(0=\beta {B \over N}(N-B)- \gamma B\)

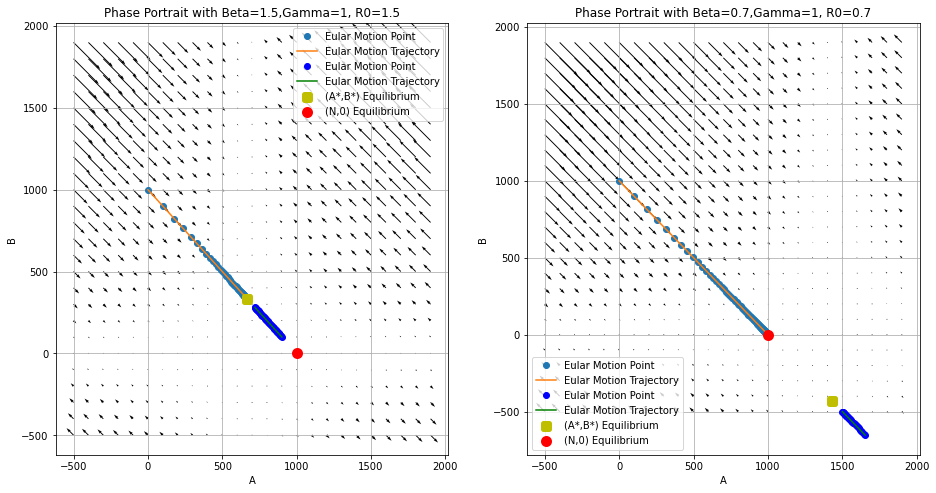
If we have \(R_0={\beta \over \gamma}\), then we got \(B^*=N(1-{1 \over R_0})\)

According to the above Phase Portrait, we can find that there are two equilibria points. The first one is \((A^,B^)\) which will change by different \(R_0\) input, and the second is (N,0) follow by N. Also We can define the following Jacobian matrix J, to analyse the stability of equilibria points.

\(J(A,B)=[\begin{matrix} {\partial f_A={\partial \dot{A} \over \partial A}} &{\partial f_B={\partial \dot{A}\over \partial B}} \\ {\partial g_A={\partial \dot{B}\over \partial A}} & {\partial g_B={\partial \dot{B}\over \partial B}} \end{matrix}]\) \(=[\begin{matrix} {2\beta A\over N}-\beta-\gamma &{2\beta B\over N}-\beta+\gamma \\ {-2\beta A\over N}+\beta+\gamma &{-2\beta B\over N}+\beta-\gamma\end{matrix}]\)

First, for \((A^,B^)\) we can get a new Jacobian matrix \(J(A^*,B^*)=[\begin{matrix} \gamma -\beta & \beta-\gamma \\ \beta-\gamma &\gamma-\beta \end{matrix}]\)

Then we can get the eigenvalues for \(J(A^,B^)\): \(\lambda_1=-2(\beta -\gamma), e_1=[\begin{matrix} 1\\1\end{matrix}]\) \(\lambda_2=0, e_2=[\begin{matrix} 1\\-1\end{matrix}]\)

So, we can get equilibria \((A^,B^)\) is, Stable, when \(\beta >\gamma\), \(\lambda =(-\infty, 0)\). Unknown, when \(\beta =\gamma\), \(\lambda =(0,0)\). Unstable, when \(\beta <\gamma\), \(\lambda =(0, \infty)\).

Second the new Jacobian matrix for \((N,0)\) is \(J(N,0)=[\begin{matrix} \beta-\gamma & \gamma -\beta \\ \gamma-\beta &\beta-\gamma \end{matrix}]\)

For the eigenvalues are: \(\lambda_1=2(\beta -\gamma), e_1=[\begin{matrix} 1\\1\end{matrix}]\) \(\lambda_2=0, e_2=[\begin{matrix} 1\\-1\end{matrix}]\)

So, the equilibria for (N,0) is, Stable, when \(\beta <\gamma\), \(\lambda =(-\infty, 0)\). Unknown, when \(\beta =\gamma\), \(\lambda =(0,0)\). Unstable, when \(\beta >\gamma\), \(\lambda =(0, \infty)\).